Heisenberg’s Uncertainty Principle

Single Slit, Hydrogen Atom & Bose-Einstein Condensates

What does Heisenberg's Uncertainty Principle actually state? Is it the result of disturbances created during the process of measurement or is it a statement derived from the most fundamental principles in quantum mechanics (and hence applies regardless of measurement)?

Full script:

0. Intro

Hi guys, how are you? It is lovely to back with some brand new stuff; this time we’ll be covering the very foundations of quantum mechanics. Isn’t that super exciting? To start with – since there is so much misinformation surrounding this topic – I decided to make a whole new series covering Heisenberg’s Uncertainty Principle.

This is a series for everybody, from beginners to more advanced levels – no matter how little or how much you already know, I am hoping you’ll find something that catches your interest. You are now watching the first video in the series; we’ll start with a little home experiment, we’ll then cover some theory and finally, we’ll finish with a few very interesting examples. I hope you enjoy it… let’s get started!

1. The Uncertainty Principle in Action (Easy Home Experiment!)

Let’s start with a little experiment to demonstrate Heisenberg’s Uncertainty Principle which can be easily set up at home and it is cheap and fun to do. We are going to need a laser pointer, a couple of very sharp blades, a clothes peg and some playdough. In addition, we will also need a smooth wall to act as our projector screen, where the laser will be fired.

Ok, so here’s the setup. As you can see, the playdough is being used to hold the laser pointer in place and also to hold the two blades in place. It will allow us to move the blades so that the distance between them can be modified at will. The clothes peg is simply being used to press the “on” button down so we don’t have to use our hands.

Now, once we have pointed the light beam right in the middle between the two blades, we can then proceed to narrow the slit’s width by slowly bringing the two blades towards each other. Be extra careful because those blades are very sharp and I’m guessing you don’t want to end up injuring yourself. So – unlike what my son is doing in this clip – try your best to keep the blades as parallel to each other as you possibly can while very slowly binging them closer together. Now, let’s pay attention to what happens to the laser spot on the wall as we make the distance between the blades narrower and narrower.

At first – as expected – the red dot gets smaller as we make the slit smaller. However, at a certain point something remarkable happens. As we make the slit even narrower, the spot begins to spread out, it starts to get wider and wider. In addition, some very interesting fringes start to appear. What is going on here?

As you may know, the wave nature of light – in particular the phenomenon of interference – is the reason why these series of light and dark fringes are created. However, the quantum mechanics behind the creation of these fringes is material for another series altogether. Here we are going to focus on how the Uncertainty principle can explain the counter-intuitive fact that the area where the photons land becomes wider and wider as we narrow the slit’s width past a certain point. But first, a little bit of theory. 

2. Heisenberg’s Uncertainty Principle

Alright… so now that we’ve seen the uncertainty principle in action, let’s find out what it actually states. Heisenberg’s Uncertainty Principle asserts that:

“In any system, in any state, the uncertainties of position and momentum obey the following inequality:”

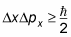
…which states that the product of the uncertainty in position and the uncertainty in momentum is always larger than or equal to this other quantity, h-bar over two, where h is Planck’s constant. (ħ is the reduced Planck constant, equal to h / 2π)

Ok, so how can we rephrase this so that it can be understood in a more intuitive way? Well, let’s say the system in question is a particle for instance – like an electron or a photon – then the uncertainty principle can be re-stated like this:

“It is impossible to find a state in which the particle has definite values for both position (x) and momentum (px)”

Two points to clarify here: one, momentum (symbolised by the letter p) is equal to mass times velocity, and since velocity has a direction, so does momentum. Which brings me to my second point: position and momentum components need to be along the same directional axis for the uncertainty principle to apply. See that little x next to the momentum symbol? It basically means that – in this case – we are talking about momentum along the x direction. And since the uncertainty principle applies to any possible directional axes, we can write with equal confidence the following inequalities for the y and z axes:

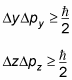
Question: Does Heisenberg’s Uncertainty principle apply to the following relationships?

The answer is absolutely not. There is no constrain on pairs of position and momentum components along different directions. Their product doesn’t obey any inequality and can, in principle, be equal to zero.

So, what does the uncertainty principle actually tell us? It tells us that it is impossible – not just hard or difficult – but that it is impossible to find a quantum state in which the particle has well-defined values for both position and momentum (and remember, we are talking about components along the same axes here). Put another way, because there doesn’t exist a state with definite values for both position and momentum, there is a fundamental limit to the precision with which the position and the momentum of a particle can be simultaneously known. We can’t know them both at the same time for the simple reason that well-defined values of both variables cannot exist simultaneously.

The uncertainty principle is a result of profound importance in quantum mechanics. Let me emphasise something: contrary to popular belief and to what some books or teachers might tell you, Heisenberg’s Uncertainty Principle is not the result of disturbances created through the process of measurement, neither it is a limitation resulting from poor instrumental precision, nor it is a reflection of our failure to gain knowledge about how Nature works. No, none of that is true. The uncertainty principle is in fact a result which can be derived theoretically from the fundamental principles of quantum mechanics, principles which describe an inherent indeterminacy in the relationship between certain pairs of complementary variables, such as position and momentum. The uncertainty principle is inherent in the properties of wave-like systems, and since quantum mechanics describes quantum entities as probabilistic waves, indeterminacy naturally arises. More on this later in another video.

3. Some Examples of Heisenberg’s Uncertainty Principle

Now, let’s take a look at the Uncertainty Principle through a couple of examples, starting with the single-slit laser experiment I showed you at the start of the video.

a) The Single Slit Diffraction Experiment

This is a diagram of the single-slit diffraction experiment, which I demonstrated earlier on. The photons in the laser beam have a momentum of magnitude p moving in the x direction, that is, perpendicularly to the slit, which has a width w measured in the y direction.

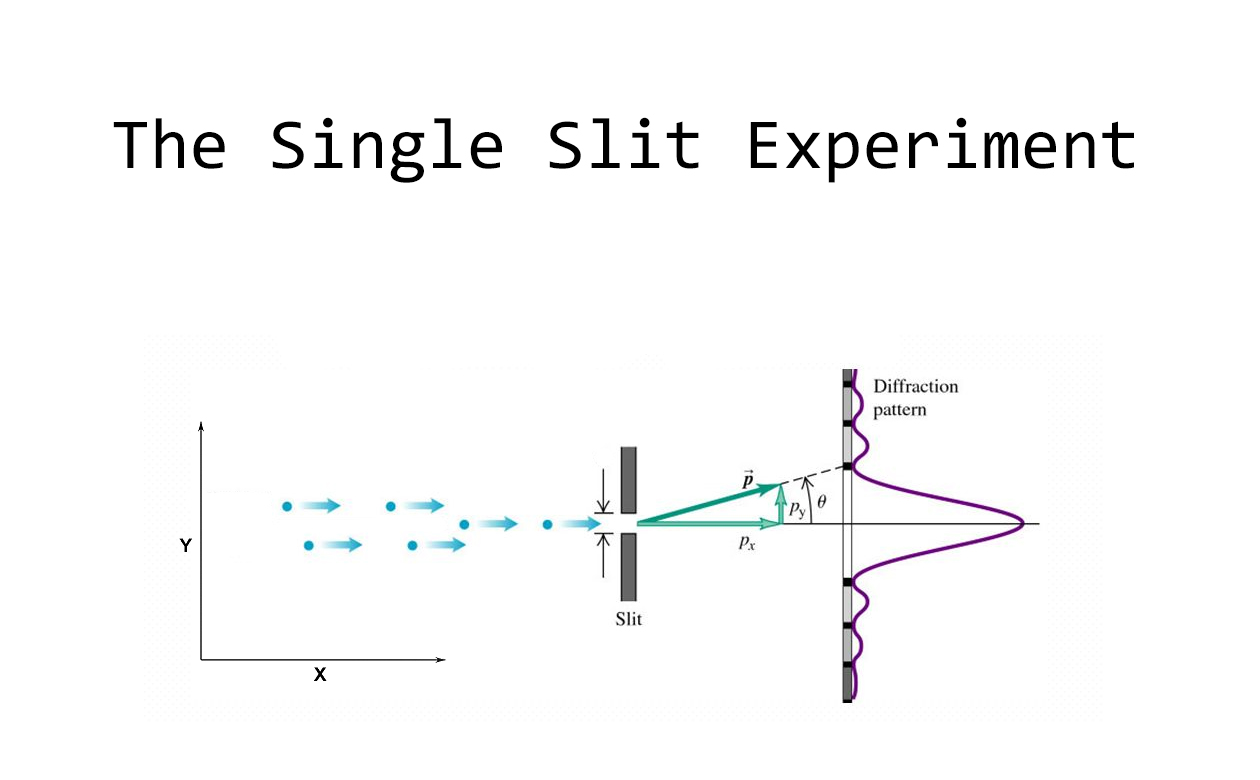
Now, let’s consider one single photon. Whereas in front of the slit the photon has definite momentum p in the x direction (and hence zero momentum in the y direction), behind the slit the situation completely changes. The restriction imposed by the slit means that the photon’s position is now known to an accuracy of at least w in the y-direction. Hence the width of the slit – w – may be taken as the photon’s position uncertainty in the y-direction, that is, we can write Δy = w.

Applying Heisenberg’s uncertainty principle now – remember, we need to apply it in the same direction, in this case, the y-axis – we get a non-zero momentum uncertainty, Δp_y  ≥   ħ/(2w) _, which means that – from behind the slit onwards – the photon’s momentum may end up having a non-zero component in the transversal direction. And this is why – for a sufficiently narrow slit – as we look at the wall, we may find the photon appearing somewhere further to the right or to the left of where we would intuitively expect it to appear. As we narrow the slit more and more, we realise that the more we try to localise the photon (that is, the more we try to define its position) by shrinking the slit’s width w, the more spread (the more uncertainty) there is in its transversal momentum.

When we consider all the photons present in the laser beam, this spread in the uncertainty of each of their momenta manifests as an angular spread in the beam behind the slit, a broadening of the diffraction pattern, which is precisely what we saw in our experiment!

b) Size and stability of the Hydrogen Atom

Here’s another interesting example. Heisenberg’s uncertainty principle not only helps to predict the approximate size of the hydrogen atom, but it also explains why atoms are stable. According to classical ideas based exclusively on Maxwell’s equations of electromagnetism, the negatively charged electron should continuously emit electromagnetic radiation, since it is constantly accelerating in its circular orbit. The electron should, therefore, spiral towards the nucleus of the atom. However, Heisenberg’s uncertainty principle prevents this from happening. Why?

Well, if the electron were to spiral in towards the nucleus, its position would become more and more precisely known, to the point where, if the electron was really close to the the nucleus, its position would be known with such a precision that – by Heisenberg’s Uncertainty Principle – the uncertainty in the electron’s momentum would have to increase by a massive factor, so massive that the electron’s kinetic energy would increase by a factor of around 10 to the power of 10. There is no way for the electron to gain this amount of kinetic energy; it is impossible since its electrostatic potential energy is nowhere near such high values, and by conservation of energy therefore, this cannot happen. And this is how Heisenberg’s Uncertainty principle explains why the hydrogen atom is the size it is and the fact that it is stable.

c) Does Heisenberg’s Uncertainty Principle apply to macroscopic objects?

You may wonder whether quantum mechanics applies just to the world of tiny things. The answer is definitely not: quantum mechanics – including the uncertainty principle – applies to everything, no matter what size. The reason why we do not usually observe the uncertainty principle in the macro-world of everyday objects is because of Planck’s constant, h, which is incredibly small; so minute that the indeterminacy imposed by the uncertainty principle becomes very significant in the realm of atomic and subatomic physics but it rarely becomes apparent in everyday life.

Having said that, there are indeed very interesting cases where the strange world of quantum mechanics does manifest in an obvious way in macroscopic objects. For instance, have you ever heard of Bose-Einstein condensates? A Bose-Einstein condensate is a state of matter obtained by cooling down a gas of atoms of extremely low density to a very, very low temperature. In order to keep the sample cool, the gas is trapped in a small volume of empty space by magnetic fields and beams of light; this keeps it away from the relatively warm walls of the container. This fascinating state of matter was first predicted by Albert Einstein and Satyendra Nath Bose in 1925, although it was not until 1995 that the first condensate was successfully produced in the lab.

This figure shows the velocity distribution profile of the cloud of gas as it is cooled down below 400 nano-Kelvin degrees.

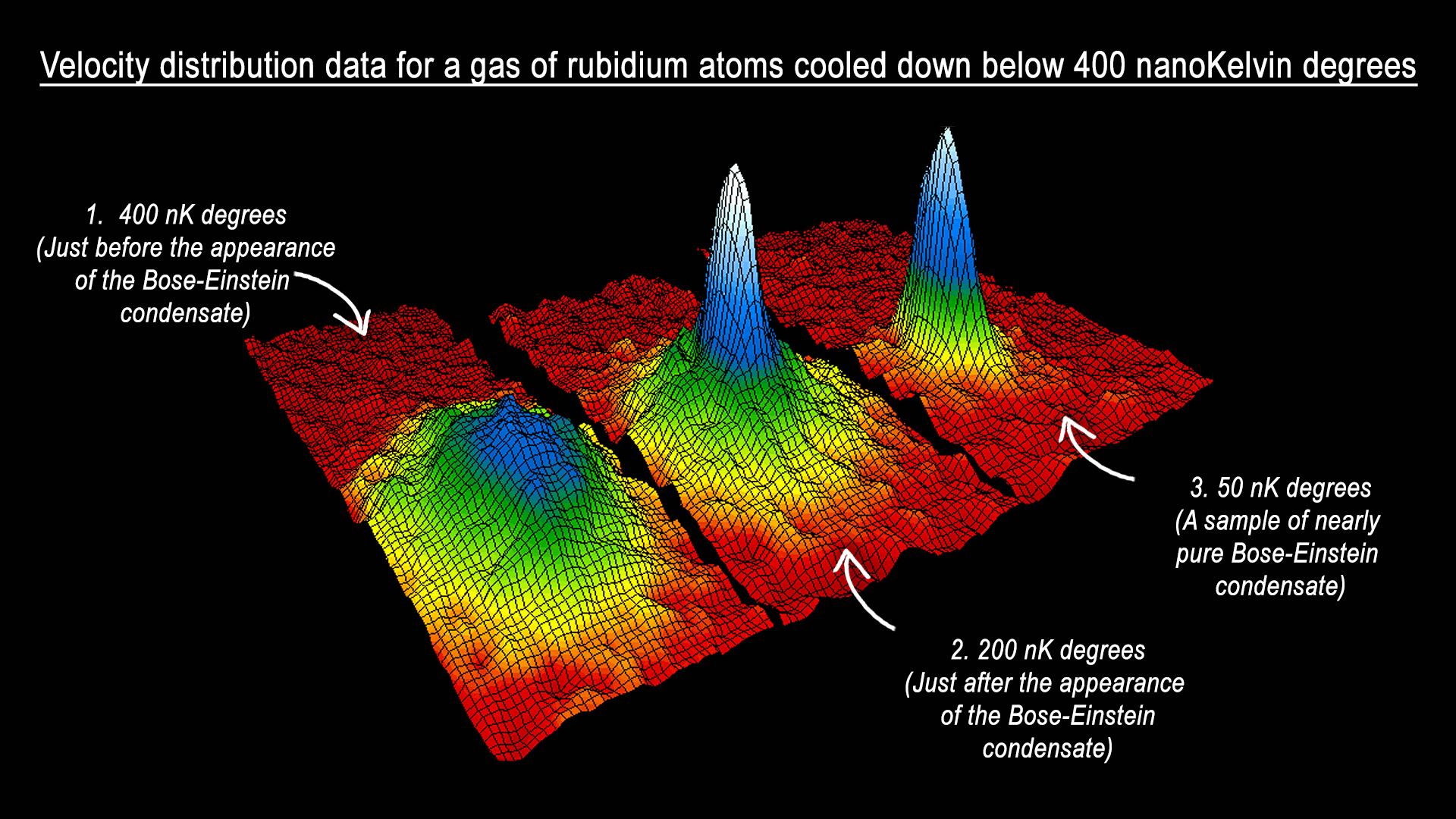
The peak that starts emerging below this temperature reveals the remarkable phenomenon known as Bose-Einstein condensation, in which a large proportion of the atoms suddenly occupy a single quantum state, and this is precisely where macroscopic quantum phenomena suddenly become apparent. The colours indicate the number of atoms at each velocity, with red being the fewest and white being the most. The areas appearing white and light blue are at the lowest velocities.

Well, it turns out that the spread of velocities – and hence momenta – in the peak is found to be close to the minimum allowed by the uncertainty principle. That is, spatially confined atoms – where their position is known with accuracy – have a minimum spread of momenta distribution, below which the uncertainty principle would be violated. On closer inspection, the peak is observed to be anisotropic, with a greater spread of momenta in one direction than another. This can be explained by the fact that the trapping region where the atoms are confined is itself anisotropic. The direction with the widest spread of momenta is that with the narrowest spatial confinement, just as one would expect from the uncertainty principle.

… to be continued

Thank you so much for watching, I hope you’ve enjoyed watching this video as much as I’ve enjoyed making it. There’s two or perhaps three more videos coming in this series covering yet more fascinating ideas around Heisenberg’s Uncertainty Principle. I am currently working on the scripts and the next video should be ready in a few weeks. In the meantime, think of this:

Quantum Mechanics, Lasers and Bose-Einstein Condensates… How about using these three ingredients to actually find out how to build a proper lightsaber? Not this… but one these? I am currently making a little extra video for you, which will be available very soon so stay tuned! Don’t forget to like, comment, share and subscribe. And last but not least, thank you so much to all my patrons and also to all of you who have recently donated via Paypal. I wouldn’t be here without your help so thank you ever so much for your support and hopefully see you very soon!

More info: Wikipedia – Heisenberg's Uncertainty Principle

** Are you willing to support my channel by becoming a patron?

http://www.patreon.com/crackingthenutshell

** Or… how about a Paypal Donation?

https://crackingthenutshell.org/donate

Thank you for your support! 🙂