Intro to Information Theory: Claude Shannon, Entropy, Redundancy, Data Compression & Bits
Script:
Summary of Previous Video:
In the previous video I discussed several definitions of information and I mainly concentrated on Gregory Bateson’s definition, which describes information as “a difference that makes a difference”. I modified his definition to information is a “perceived difference that can make a difference” and discussed how information has the potential to be used as the basic currency for describing reality.
Reality is a subjective experience, it is perception, it is qualia. In this way, information represents the connection between the observer and the observed, it encapsulates the link between the subject and the object, the relationship between what we conceptualise as the external world and what it feels like to experience this external world from within.
Therefore, using information to describe reality also embodies the recognition that, in many contexts, it doesn’t make sense anymore to speak of things in themselves, but that all we can possibly describe are perceived distinctions, perceived properties, perceived patterns and regularities in Nature.
Information has the potential to be assigned a meaning and therefore it has the potential to become knowledge. Meaning is subjective so information doesn’t really have objective intrinsic meaning.
Introduction to Information Theory:
Now, you may be wondering what science has to say about all this. How does science currently define information? Has science been able to objectively quantify information? The answer to these questions lies at the heart of Information Theory.
Information Theory is a branch of mathematics and computer science which studies the quantification of information. As you have probably realised by now, the concept of information can be defined in many different ways. Clearly, if we want to quantify information, we need to use definitions which are as objective as possible.
While subjectivity can never be completely removed from the equation (reality is, after all, always perceived and interpreted in a subjective manner) we will now explore a definition of information that is much more technical and objective than the definitions we discussed in the previous video.
This is Claude Shannon, an American mathematician and electronic engineer who is now considered the "Father of Information Theory". While working at Bell Laboratories, he formulated a theory which aimed to quantify the communication of information.
Shannon's article titled "A Mathematical Theory of Communication", published in 1948, as well as his book "The Mathematical Theory of Communication", co-written with mathematician Warren Weaver and published in 1949, truly revolutionised science.
Shannon's theory tackled the problem of how to transmit information most efficiently through a given channel as well as many other practical issues such as how to make communication more secure (for instance, how to tackle unauthorised eavesdropping).
Thanks to Shannon's ideas on signal processing, data compression, as well as data storage and communication, useful applications have been found in many different areas. For instance, lossless data compression is used in ZIP files, while lossy data compression is used in other types of files such as MP3s or JPGs. Other important applications of Information Theory are within the fields of cryptography, thermal physics, neurobiology or quantum computing, to name just a few.
It is important to realise that Shannon's Theory was created to find ways to optimise the physical encoding of information, to find fundamental limits on signal processing operations. Because of this, Shannon's definition of information was originally associated with the actual symbols which are used to encode a message (for instance, the letters or words contained in a message), and not intended to relate to the actual interpretation, assigned meaning or importance of the message.
As we have seen in the previous video, information itself does not really have intrinsic objective meaning. What Shannon's Theory aimed to tackle were practical issues completely unrelated to qualitative properties such as meaningfulness, but more related to the actual encoding used in the transmission of a particular message.
Therefore, what we are dealing with here is a very different definition of information than those we have discussed so far. Shannon defines information as a purely quantitative measure of communication exchanges. As we will see, Shannon's definition represents a way to measure the amount of information that can potentially be gained when one learns of the outcome of a random process. And it is precisely this probabilistic nature of Shannon's definition that turns out to be a very useful tool; one that physicists (and other science disciplines) now use in many different areas of research.
Shannon's information is in fact known as Shannon's entropy (Legend says that it was the mathematician John von Neumann who suggested that Shannon use this term, instead of information). In general, I will refer to Shannon's definition as Shannon's entropy, information entropy or Shannon's information, to avoid confusion with other definitions of information or with the concept of thermodynamical entropy.
Shannon's Entropy Formula – Uncertainty – Information Gain & Information Content:
So what is Shannon's definition then? Well, the amount of information contained in a given message is defined as the negative of a certain sum of probabilities. Don't worry, we are not going to deal with the actual details of the equation here, but instead I will give you a flavour of what it means. Suppose we have a probabilistic process which has a certain number of possible outcomes, each with a different probability of occurring.
Let's call the total number of possible outcomes N and the probabilities of each outcome p(1), p(2), p(3), ….., p(N). For instance, let's say that the probabilistic process we are dealing with is the throw of a coin. In this case, the total number of possible outcomes is 2, so N=2 (that is, heads and tails – let's call heads 1 and tails 2). The probabilities associated with each of these possible outcomes, assuming a fair coin, is ½. So we have p(1)= ½ and p(2)= ½ (which is the same as saying each possible outcome, heads or tails, has a 50% probability of occurring).
Shannon showed that the entropy (designated by the letter H) is equivalent to the potential information gain once the experimenter learns the outcome of the experiment, and is given by the following formula:
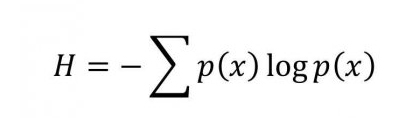
This formula implies that the more entropy a system has, the more information we can potentially gain once we know the outcome of the experiment. Shannon's entropy can be thought of as a way to quantify the potential reduction in our uncertainty once we have learnt the outcome of the probabilistic process.
Don't worry if you feel a bit confused right now. I'll explain the concept of Shannon's entropy for you in very easy terms. Let's go back to the coin example:
The coin is fair, so the probability of heads is the same as the probability of tails (that is, ½ each). Let's consider the event of throwing the coin. Plugging the given probabilities into the equation gives us a Shannon entropy, that is, an information content of one bit, because there are two possible outcomes and each has equal probability. Once we have thrown the coin and we have learnt its outcome, we can say that we have gained one bit of information, or alternatively, we can say that our uncertainty has been reduced by one bit.
Now imagine you have a coin which has two heads. In this case, N=1, that is, there is only one possible outcome. The likelihood of obtaining heads is therefore equal to 1 (a probability equal to 1 means absolute certainty, 100%). Since the uncertainty is zero in this case, Shannon's entropy is zero, and so is the information content. There is no longer the presence of two different alternatives here. The information we gain after throwing the coin is therefore, zero. Look at it this way: we already knew with certainty what was going to happen in advance, so there is no potential gain in information after learning the outcome.
Another way of describing Shannon's entropy is to say that it represents the amount of information the experimenter lacks prior to learning the outcome of a probabilistic process.
Hence, according to Shannon's formula, a message's entropy is maximised when the occurrence of each of its individual parts is equally probable. What this means is that we will gain the largest amount of Shannon's information when dealing with systems whose individual possible outcomes are equally likely to occur (for instance, throwing a fair coin or rolling a fair die, both systems having a set of possible outcomes which are all equally likely to occur).
Shannon's entropy is a measure of the potential reduction in uncertainty in the receiver's knowledge. We can see the process of gaining information as equivalent to the process of losing uncertainty. You may be wondering what all this has to do with the actual content and encoding of a message, since so far we have only been talking of coins. Here's another example, which illustrates the usefulness of Shannon's formula when it comes to written language.
Entropy per Character – Written English Language:
Can we estimate the information entropy of the written English language? Consider starting with one particular letter which is picked at random. Knowing this first letter, you then want to estimate the probability of getting another particular letter after that one, and the probability of getting another letter after that first and second one, and so on. Knowing these probabilities is what we need in order to calculate the information entropy associated with the English text.
If we assume we are dealing with 27 characters (that is, 26 letters plus space), and that all of these characters are equally probable, then we have an information entropy of about 4.8 bits per character. But we know that the characters are not equally probable; for instance, the letter E has the highest frequency of occurrence, while the letter Z has the lowest. This is related to the concept of redundancy, which is nothing more than the number of constraints imposed on the text of the English language: for example, the letter Q is always followed by U, and we also have rules such as "I before E except after C", and so on.
There are various methods for calculating the information entropy of the written English language. For instance, Shannon's methods – which take into account many factors, including redundancy and contextuality for instance – give the English language text an information entropy of between 0.6 and 1.3 bits per character.
So, if we compare this with the previous result of around 4.8 bits per character, we can see that the constraints imposed by factors such as redundancy have the overall effect of reducing the entropy per character. What this means is that finding the amount of redundancy in a language can help us find the minimum amount of information needed to encode a message. And of course, this leads us to the important concept of data compression.
Data Compression – Redundancy:
In information theory, the redundancy in a message is the number of bits used to encode it minus the number of bits of Shannon’s information contained in the message.
Redundancy in a message is related to the extent to which it is possible to compress it. What lossless data compression does is reduce the number of bits used to encode a message by identifying and eliminating statistical redundancy . Hence:
The more redundancy there is in a message, the more predictability we have à that means less entropy per encoded symbol à hence the higher the compressibility
When we compress data, we extract redundancy. When we compress a message, what we do is encode the same amount of Shannon’s information by using less bits. Hence, we end up having more Shannon’s information per encoded symbol, more Shannon’s information per bit of encoded message. A compressed message is less predictable, since the repeated patterns have been eliminated; the redundancy has been removed.
In fact, Shannon’s entropy represents a lower limit for lossless data compression: the minimum amount of bits that can be used to encode a message without loss. Shannon's source coding theorem states that a lossless data compression scheme cannot compress messages, on average, to have more than one bit of Shannon’s information per bit of encoded message.
Calculating the redundancy and the information entropy of the English language has therefore many practical applications. For instance, ASCII codes (which are codes that represent text in computers, communications equipment, and other devices that use text) allocate exactly 8 bits per character.
But this is very inefficient when we consider Shannon's and other similar calculations which, as we have seen, give us an information entropy of around 1 bit per character. Put another way, a smaller amount of bits can be used to store the same text. What this means, is that, in theory, there exists a compression scheme which is 8 times more effective than ASCII.
Let’s use an example to see how lossless data compression works. We will use Huffman coding, an algorithm developed by electrical engineer David Huffman in 1952. Huffman coding is a variable length code which assigns codes using the estimated probability of occurrence of each source symbol. For instance, let’s say we take as symbols all the letters of the English alphabet plus space. Huffman coding assigns codes with varying length depending on the frequency of occurrence of each symbol. Just as with Morse code, the most frequent symbols are assigned the shortest codes and the less frequent symbols are assigned the longest codes.
Let’s take a piece of text written in English, which is long enough so that we can approximate our calculations by using standard frequency tables for the letters of the written English language. The most frequent symbols, such as space and the letter e will be assigned the shortest codes, while the least frequent symbols, such as the letters q and z will be assigned the longest codes. Applying the Huffman algorithm using standard frequency tables, we obtain the Huffman codes given on this table. As you can see, the lengths of the codes vary from 3 to 11 bits, depending on the character.
We are going to use this short passage, from Brave New World, by Aldous Huxley:
“All right then," said the savage defiantly, I'm claiming the right to be unhappy."
"Not to mention the right to grow old and ugly and impotent; the right to have syphilis and cancer; the right to have too little to eat, the right to be lousy; the right to live in constant apprehension of what may happen tomorrow; the right to catch typhoid; the right to be tortured by unspeakable pains of every kind."
There was a long silence.
"I claim them all," said the Savage at last.”
Excluding punctuation and just counting letters and spaces, we have a total of 462 characters to encode. If we encode this piece of text using ASCII, we will need to use a total of 3,696 bits (8 bits per character). However, if we use Huffman code, we will only need to use a total of 1,883 bits (an average of about 4.1 bits per character).
So we see that by using Huffman encoding instead of ASCII, we can store the same amount of information, but twice as effectively. Although Huffman coding is more efficient, we are still far from reaching the limit given by Shannon’s entropy, which as we saw earlier on, can be approximated to be around 1 bit per character.
By using Huffman’s code, we have managed to extract a certain amount of redundancy, but we are still far from the limit where all the redundancy would have been extracted: that limit is Shannon’s entropy.
There are however many other compression techniques; for instance, there is a technique called arithmetic coding, which can extract a lot more redundancy than Huffman coding, and hence it can create compressed messages where the average number of bits per character is much closer to Shannon’s entropy.
So by using this particular example, we have seen how the concept of Shannon's entropy, in this case calculated from the probabilities of occurrence associated with the letters belonging to the words of a particular language, has very important applications; data compression being one of them. Summarising:
Shannon's entropy is a measure of uncertainty, of unpredictability, and also a measure of information content, of potential information gain.
Shannon’s entropy can also represent a lower limit for lossless data compression: the minimum amount of bits that can be used to encode a message without loss.
Also note that with this definition, more information content has nothing to do with its quality. So in this sense, a larger amount of Shannon's entropy does not necessarily imply a better quality of its content (an example of two subjective concepts which could be linked to quality are meaningfulness or importance).
I will expand on this topic in the following video, when we discuss Norbert Wiener’s ideas.
Shannon's Bit vs Storage Bit:
Now, there is one point that needs clarifying. In this past section of the video, while discussing concepts such as compression and redundancy, we have actually been talking about different kinds of bits, that is, bits which represent different concepts.
You may recall that in the previous video we defined the bit as a variable which can have two possible values, which we represent by the digits 0 and 1. This is the most popular definition, one that is usually associated with the storage or transmission of encoded data. In this way, one bit is the capacity of a system which can exist in only two states.
In information theory, however, the bit can be defined in a different way. As we have seen, it can be a unit of measurement for Shannon’s information. In this context, one bit is defined as the uncertainty associated with a binary random variable that can be in one of two possible states with equal probability.
Put another way, one Shannon bit is the amount of entropy that is present in the selection of two equally probable options, it is the information that is gained when the value of this variable becomes known. Remember, this is exactly what we showed earlier on when we applied Shannon’s formula to the throw of a fair coin.
Well, it turns out that the first time the word “bit” appeared in a written document was precisely in Shannon’s ground-breaking paper “A mathematical theory of communication“. In it, Shannon clearly states that it was mathematician John Tukey, a fellow Bell Labs researcher, who coined the term “bit”, short for binary digit.
While Tukey’s binary digit is a unit related to the encoding of data, Shannon’s bit is a unit that is related to uncertainty, unpredictability. In one Tukey bit of encoded data there is often less than one bit of Shannon’s information. Why?
Well, Shannon’s entropy is maximised when all possible states are equally likely, and one Shannon bit is defined in relation to a system whose states are equally likely. Therefore, in a binary system, when the two possible states are not equally likely, such as the toss of a biased coin, Shannon’s information is less than 1 bit.
Recall Shannon's source coding theorem, which states that a lossless data compression scheme cannot compress messages, on average, to have more than one bit of Shannon’s information per bit of encoded message. Well, now you know that these bits are different kinds of bits, in the sense that they represent different concepts. The latter refers to the encoding, storage or transmission of binary data, redundant or not, whereas the former refers to amounts of Shannon’s information, as defined by his entropy equation. An encoded bit of data contains, at most, one bit of Shannon’s information, usually a lot less.
In information theory, therefore, it is important to understand the distinction between encoded binary data and information. In this context, the word information is used in reference to Shannon’s entropy, a much more abstract concept that does not equate with the actual encoding of zeros and ones.
Now, so far we have discussed the important concepts of entropy, uncertainty, information and redundancy… and we have seen how Shannon’s Source Coding Theorem provides us with a theoretical lower bound for data compression. Hopefully you now understand the relationship between entropy, uncertainty reduction, information gain, information content, redundancy and compression.
We have covered the most important theoretical aspects of Information Theory which establish the limits to how efficiently a particular message can be encoded.
But what does Shannon have to say about sending a message not only efficiently but also reliably though a given channel? How does one transmit information reliably in the presence of noise? That is, in the presence of physical disturbances which can introduce random errors in the encoding of a particular message, what are the theoretical limits to detecting and correcting these errors? This leads us to the very important topic of Error-Detection and Correction.
… to be continued 🙂
Coming up in Part 2b:
– Shannon’s Noisy Channel Coding Theorem
– Adding redundancy bits to a message (called parity or check bits) to detect and correct errors
– Error-correcting codes – What are Hamming codes?
– Example using a Hamming code
– What are doubly-even self-dual linear binary error-correcting block codes?
– James Gates discovery: error-correcting codes found buried inside the fundamental equations of physics?
– Little side journey: Cosmological and biological evolution. The Universe as a self-organised system. How does Nature store information? Nature’s use of redundancy and error-correcting codes. Information, the Laws of Physics and unknown organising principles: fixed or evolving? Biology, DNA and information.
References – Further Information:
Princeton Uni: Shannon's Entropy
Entropy, Compression & Information Content – Victoria Fossum
Entropy & Information Gain Lecture – Nick Hawes (very good at clarifying difference between individual information of each outcome and the expectation value of information, that is, Shannon’s entropy)
Harvard Uni: Entropy & Redundancy in the English Language
Lecture: Entropy & Data Compression – David MacKay
Documentary: Claude Shannon: Father of the Information Age
Video: Entropy in Compression – Computerphile

I would like to thank you deeply your effort about doing this compilation, I think you´ve a special sensibility for the subject, it isn´t easy, so it´s great that someone is explaining this step by step, I´m starting to do a research about the work of Shannon and Silvester James Gates, I want to go carefully trying to establish the right relations in this matter. You´re a good example in this. I would like to share some thoughts that came to me after watch your videos.
Notice that Silvester James Gates is linking his research into the Adinkra symbols to the geometrical patterns, better said, he is linking “some kind” of information to a patterns that he call “matrices”, as they appeared at the end of his video “ Does Reality have a Genetic Basis?”, well the question of the geometry is important if we can identificate it as related with the natural world or is a ideal model that has nothing to do with the natural world. For example the Golden number (Phi) and the Fibonacci sequence is clearly related to the natural world but the hypercube (the geometry related to the work of S.J. Gates) is not, the hypercube is an idealization (as far I can understand), a geometrical construct to explain in a metaphorical way the projection of the four dimension.
So here should be the first point to think about, there are geometrical patterns directly related to the natural world, and other are artifical constructs to explain scientific concepts. In the case of S.J.Gates the hypercube is related to the second kind of geometry, the hypercube seems don´t exist in the natural world. As well this is happening with the concept of the information.
Well, we have something to deal here… I´m expecting if the community of science decide to support the work of S.J.Gates, maybe they´ll do or maybe not, the important thing here (I think) it´s not determine right now if he is in the right path, he seems to be great physicist but we're dealing with an hypothesis of a theory and some philosophical issues too.
The information, as I understand it, can have two fundamental branches:
1. Abstract or artificial (the kind of information that we create, in a computer o text for example) This is (mostly, maybe) not physical and is as you said in the video, relative to the interpretation of the receiver. (non physical if you considered the cities as non systems of creation of information, the cities are like the shell of a nutshell…is the shell part of the information?…)
2. Natural or biological. This is (excluding the empty space in the atoms) physical, for example a natural seed of a tree (which has a “program” to develope a fractal structure) Others seeds have another kind of information to transfer, another geometrical patterns. The seed of an apple has the program for a toroidal structure growing from a pentagon. Each seed has its own “memory” that it has been shaped by a process of elimination of redundant bytes of information. Becoming a loop of life. I think that you should consider that a –nutshell– is a- seed-. And when you crack the shell you are obtaining the source of the information –the nut-. The receiver in this case the field or the terrain will interpret the nut as a seed that carry the information to convert itself a redundant complex fractal information to become a new tree with new seeds. So the redundant information in the biological context of a growing tree is the increment of possibilities or probability to create new trees.
What do you think about this?
We´re going slowly now, better, because as you have explained so well in your video, there´s the subject of the redundant bits of information. I think in the example of the seed… the nature seems have a natural process to compress information, we can call this process “implosión”, or fractal auto-recursive-creation, in a system as we lived we have different levels of material implosion information, first we need water, vegetables and animals to exist as human, so the level of interdependency maybe it´s pointing to a natural hierarchy, the machines have evolved because we have the enough support from the upper level, the biosphere, that creates its own auto-regulatory system. We shouldn´t obviate this hierarchy of existence, the interdependence between levels. Not now when the biosphere is suffering or changing in bad for us. This is a key question to manage the different planes of information as a systems that creates others systems, the evolution of the nature has allowed that exist human systems that when they thrive in a cultural and science way creates artificial information, and machines to simulate this artificial information.
The question if all this is running in a advance simulation program that we call universe, is that we can´t say in a certain way, (it could be atractive to some way of thinking but not for that should be the correct model, and we have to manage certain precaution about this “infinite” concept of the simulation, it has social implications). The ecuations of S. J. Gates are pointing an artificial structure because he is showing his result through a process of artificial mathematical symbols created by humans, so it´s reasonable considered if we use that symbols as ecuations to create logic, soon or later they are going to resemble computer code…. Why? Because these are the kind of symbols used by our brain that have allowed the existence of logical devices as machines… But it doesn´t prove that we are living in that computer code, could be that this computer code it´s a simulation itself, a metaphoric representation of the structure of the reality but not the reality itself. So, although the hypothesis of S.J.Gates could be correct at the end but it won´t demostrate that we lived in a simulation context because it isn´t dealing with the biology itself. DNA seems to work as an advance computer, and our computers are pointing to have chips like DNA as IBM is researching, but we can´t forgat from where we are taking the model and reference of the copy. The virtual reality exist, yes, but in this moment we only can say for sure that it´s inside of the machines. Maya as buddha considered it, could be more related to the prision the narrow cultural systems of belief that the human being creates and can distort his perception of reality. Is like to say that the cultural systems can fall into a loop of negative and entropy funcion for a comunity of humans, but this is related with the colective mind of a culture but not with the external world or reality that has its own rules.
What S.J. Gates says (among others) is that this thing that appeared to be around us as matter is only a simulation artifical information, but in my point of view I can´t see enough evidence to this conclusion because could be a not accurate representation of the nature of the biological information, only because we can´t understand that complexity it´s hard to say that is only a simulation. Some kind of new mystics try to promote this kind of view, and although I considered myself platonic in some ways, I can´t buy that scenario in a blindly way. Could be reduccionist as say: “God did it…” or “the great programmer did it” but that conclusion it´s be lazy to explore the answer and let the exploration of the nature of the information inconcluse. So… should we distinguish between artificial information and biological information?, I think we should. In fact our articifial information created by our own cultural systems emulate the bilogical information systems, as example you can find how different researchers are point to the DNA as a complex Turing machine. Yes, as S.J. Gates has seen in his equations the DNA can be considered a self error-correction machine, for me it isn´t a surprise that the our logic that derives in a biological evolution from the DNA drives us now to the DNA itself as almost perfect machine, a quatum-clasical machine, that is able to integrate both ways of science. Our own biological programation is the loop of knowledge that drives to discovered who we are, maybe… All the related to S.J.Gates it´s very interesting but the relation between the Adinkra patterns and the ecuations could be something to do with Rupel Sheldrake and some kind of the expression of the morphogenetic field, the question is if the human culture is able to “connect” with this field and express it through certain (not all) cultural and artistic expressions, because this self correcting codes in a final destination could be related with de DNA itself after all. Could mark the DNA the limit of logical perception o logical creation in humans as 1 bit is making the limit in Shannon´s compression of information? I don´t know, it´s just a open question. But if we finally confused the artifical information (created by us) and the biological (created, programmed by nature) and we put both as non-physical and artificial, then we´re going to favour artificial mecanical thinking and we´re not going to feel humility in front the things that we still don´t know of the nature.
I can really appreciate your comments about these thoughts.
We can point the theory if the evolution it´s process of “taking out” redundant information in the DNA, making brains more efficients, or bodies better adapted, but also can be the opposite, that the evolution hasn´t a clearly arrow of taking out the redundant of information, and could be that the ideas are the process that the nature use to create a better or worse future for all of us, of course, ideas of fear and control are going to create a very bad future, and ideas with open but critical minds with compasion are going to make us live in a better reallity. So I´m agree with you states such as meditation can help to identificate in a better way which ideas a redundant in our lives, in order to create a better vision to all us or at least for oneself, however the self itself and the information that it carry could be part of the Maya. This Maya that we confront through daily life, lucid dreams, meditations, is another part the reality that the chamanic vision try to deal with. But that is another story. Although we can perceive the infinite worlds of the dreams and others states of awareness, daily we have to deal with the finite, that doesn´t mean accept all as it is, maybe we can search inspiration in the infinite to deal with the part of our finite reallity, as a search of creativity through imagination. But we shouldn´t forget where we are.
You´re very talented explaining this in your videos. And your work is helping me to develope ideas for a new studies that I´m going to do. So continue doing what you do. I would like to know your point of view about these thoughts, because I don´t know many people that can express this with precision and positive motivation as you do in your videos. I´m waiting with expectation your new videos, sure you´re discovering new interesting relations, I hope we´ll share information and thoughts.
Congratulations and thank you, take care Dolors.
Thank you VERY much for this awesome video and excellent effort. I wonder have you made the 2b part ?
I'm really looking forward to see it.
This is a huge effort and very awesome work. I deeply congratulae you for your hardwork and thank you making so much plaisir to read this research. You really have great potentials. Good luck with your second part. Continue.
Really great effort..Am looking forward to your next 2b video!
If things go right for me, I will donate your much appreciated endeavor.
This is a great video, and a very nice introduction to the theory. However, I want to emphasize one thing.
You say: "While subjectivity can never be completely removed from the equation (reality is, after all, always perceived and interpreted in a subjective manner) we will now explore a definition of information that is much more technical and objective than the definitions we discussed in the previous video."
The subjectivity of the our perspective that defines our reality (you mention that "Reality is a subjective experience, it is perception, it is qualia") is explicit in Shannon's theory. It is the prior (in a Bayesian sense) before receiving the signal. Conditioning on the signal (in a Bayesian sense) gives the posterior, and Shannon's "information" (which in fact is different from Shannon's entropy) is the expected divergence from the posterior to the prior. So Shannon's information is fundamentally subjective becuase it is up to the receiver of the signal to define their prior distribution over the variable of interest – the variable that we gain information about by receiving the signal.
Also the receiver must know the joint distribution between the signal variable and the variable of interest. This joint distribution is usually a model, which itself is subjective. Shannon's theory does not cover this explicitly, but later adaptations do.
In summary, I do not really think it is fair to describe Shannon's concept of information as objective. It is certainly quantitative, but I do not believe that it can be described as objective. This is absolutely not a limitation of the method or theory at all. It is the nature of reality: as you correctly point out, reality is a subjective experience, as is the process of receiving information. So any theory that describes the process of receiving information must also be subjective at a fundamental level.
This is another WONDERFUL presentation. THANK YOU!
Wow – a great review of things I partial learned or should've learned in computer science. And great work to distinguish how the data versus the informatin (via meaning of last video). I should propably listen to it again, but want to view the Time one. Have you thought about presenting at the Science and Nonduality conference ? They are looking for abstracts….
Hi, I have created a social network for people with great ideas. I'd love it if you joined and we can chat even more. http://www.noumenex.com
but it is funny that I named my site after the noumenon and here you are saying that it is not practical to think about things in themselves. Can you please explain to me if, when you said it is impractical, you meant that there is no noumenon or that from a subjective experience it is just impossible to know of the noumenon.
I'm under the impression that as subjective units of nature we intrinsically observe only some of the information of reality and that the noumenon can only be known when all information is known. the noumenon would be absolute certainty which we can only have if we know everything and so the noumenon would be everything. So yes it would be impractical to speak of noumenons as subjective units but it still exists. What do you think? Thanks
Waiting for WII (2b) video!
I love the way you explained entropy, redundancy, data compression and bits.
It helped me alot in understanding these concepts.
how to access part 2 of this video?